MATERIAIS DIDÁTICOS

É usado para estudar os sólidos geométricos, reconhecer elementos visuais, reconhecer planificações, estudo das áreas laterais, base e total, cálculo de volume, relacionar planificação ao sólido.

É um recurso didático que pode ser utilizado para o estudo da geometria e propicia a construção do conhecimento matemático através de atividades concretas, práticas e desafiadoras. É um material manipulativo que facilita o processo de ensino-aprendizagem da matemática, dando apoio e suporte à representação mental favorecendo, assim, a abstração.

Objetivo
✓ Montar um cubo 3x3x3 com sete policubos
(peças irregulares formadas com até 4 cubos).
✓ Classificar, selecionar e movimentar sobre o plano as peças que compõem os quebra-cabeças.
✓ Observar a conservação de uma forma após a realização de um movimento.
✓ Aplicar diferentes estratégias para resolução de
problemas.
✓ Completar o jogo para gerar sentimento de capacidade e influenciar o autoconceito do(a) estudante.
Dinâmica da atividade
Os mediadores deixam o estudante manipular livremente as peças dos jogos, por tentativa e erro, observando como ele usa sua lógica. Caso o estudante precise de ajuda o mediador o desafia a analisar as peças e a pensar em como elas podem ser movimentadas para serem encaixadas perfeitamente, antes de ficar colocando e retirando aleatoriamente.
Estimular o estudante a analisar quais peças são mais fáceis de encaixe e quais são mais difíceis. Separar as
mais difíceis e formar uma base (sem buracos) com elas, seguir completando com as peças restantes mais fáceis de encaixar. Não desmontar a base até que tenha tentado todas as posições das peças restantes.
Existem mais de 230 formas diferentes, fora as rotações e translações, para montar o cubo. Ao descobrir uma
forma, outras diferentes podem ser buscadas.

OBJETIVO/UTILIZAÇÃO: Para construir vários tipos de figuras geométricas, figuras simétricas, União e Intersecção, estudo do triângulo equilátero e do hexágono. Serve também, p/ Cálculo de porcentagem. No Geoplano também pode ser trabalhado o conceito de medida, de vértice, de aresta, de lado, de simetria, área, perímetro, e conceito de multiplicação nas séries iniciais, entre outros.
JOGO–BATALHA DE RETAS
Cada jogador estabelece 5 retas distintas no seu Geoplano com uma liga para cada reta essas retas podem ser na horizontal, vertical ou com inclinação de 45° para que passe pelos pinos diagonais. As retas devem ser do maior tamanho possível pelo geoplano e que passem por pelo menos 4 pinos, não podendo ficar apenas um segmento de reta.
REGRAS-
1. Na sua vez de jogar declara três pontos para o oponente se pertencem a alguma reta, o oponente deverá declarar se acertou.
2. O jogador pode eliminar uma reta de duas maneiras diferentes.
I) Acertar três pontos de uma mesma reta obtendo 3 pontos
II) Acertando dois pontos da mesma reta e apresentado a equação (ou falar quais os demais pontos da reta) obtendo 5 pontos
3. Vence quem primeiro obter 15 pontos.




Um jogo que exige raciocínio e concentração! A Torre de Hanói pode ser trabalhada em diferentes níveis de desenvolvimento as crianças: na pré-escola por exemplo, com regras simples de separação de cores e tamanhos, ajuda na coordenação motora e na identificação de formas e cores. De forma mais ampla, o jogo torre de hanói é utilizado para o estabelecimento de estratégias.
O objetivo é transferir todos os discos de uma haste para outra, mas as regras são:
– Movimentar um só disco de cada vez.
– Um disco maior não pode ficar acima de um menor.
– Não é permitido movimentar um disco que esteja abaixo de outro.




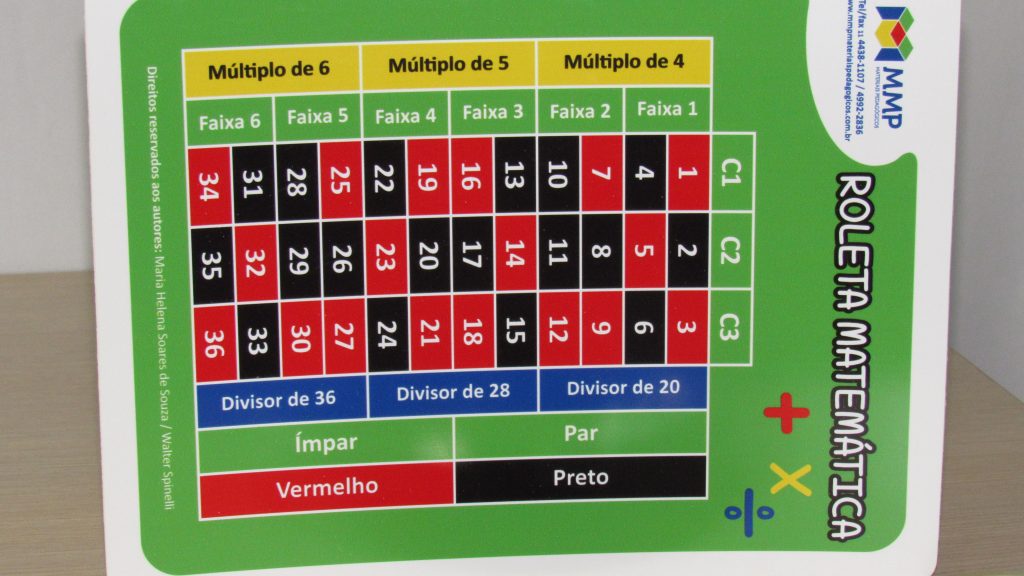
Estrutura: tabuleiro, três dados e fichas para cobrir os valores dos tabuleiros.
Objetivo:
Cobrir o maior número possível de grupos de três valores vizinhos ligados em
linha horizontal, vertical ou diagonal. Ganhará o jogo o participante que tiver obtido o
maior número de trios.
Regras:
Na sua vez de jogar, o jogador lança três dados. Com os valores resultantes,
compõe uma expressão numérica. Diz em voz alta a expressão com a sua resposta e
cobre o valor correspondente ao resultado no tabuleiro. Se na sua vez de jogar não
houver possibilidade de cobrir um número, passa a vez para o próximo jogador. O jogo
termina quando não houver mais círculos a serem cobertos.
Variação: o jogo pode acabar quando um dos participantes fizer três trios primeiro ou
pode ser determinado um tempo e, ao final deste tempo, o participante que tiver mais
trios vence o jogo.






Objetivo Pedagógico: Desenvolver habilidades com a tabuada de multiplicação
desde 1×1 até 12×12.
Regra:
1º Cada jogador escolhe uma cor de fichas.
2° Jogar os dois dadinhos e cobrir com uma de suas fichas a casa que corresponde ao produto dos números sorteados.
3º O próximo jogador lança os dadinhos e faz o produto dos valores sorteados. Se a casa correspondente a esse valor estiver vazia ele coloca sua ficha sobre ela; se estiver uma ficha do adversário, ele tira e coloca sua ficha no lugar e passa a vez.
4º O jogo se sucede até que um dos jogadores complete quinze casas com suas fichas.
5º Quem completar primeiro é o vencedor.




O Cubo da Soma é um quebra-cabeça, e consiste em um conjunto de oito peças tridimensionais, formadas pela união de pequenos cubos, combinadas de forma a criar um cubo maior.
É um jogo didático excelente para mostrar o cubo da soma de dois termos
(a + b)³.
Com esse material de apoio também podemos estudar as relações algébricas, como colocar um fator em evidência, estudo de volume, etc.


Descrição
Este jogo não difere muito do dominó clássico. É composto por 28 peças, divididas em duas partes cada. Cada parte é numerada de 0 a 6. A única diferença entre o Dominó Equacional e o clássico é que no novo jogo o número está escondido em uma equação do primeiro grau, isto é, é a solução da equação indicada.
1-A sala deve ser dividida em 4 grandes grupos, cada um com aproximadamente 8 alunos. Em cada grupo, devem ser formadas 4 duplas.
2-Cada grande grupo fará um jogo. No jogo, após serem embaralhadas, são distribuídas 7 peças a cada dupla. Os dois parceiros devem cuidar para que seus oponentes são vejam suas peças.
3-Inicia o jogo a dupla que tiver o carretão de 6. Depois, decide-se a ordem de jogada que for mais conveniente entre as duplas.
4-Em cada jogada, a dupla deve colocar uma de suas peças que tiver uma das soluções das extremidades da fileira a ser formada no jogo.
5-Caso a dupla não tenha peças com a solução de nenhuma extremidade da fileira, passa-se a vez para a próxima dupla.
6-Caso nenhuma dupla tenha peças com uma das soluções das extremidades, entra-se num consenso de se abrir a fileira em algum ponto para continuar o jogo.
7-Vence o jogo a dupla que estiver sem nenhuma peça ou, se não houver tempo, a que tiver menor quantidade de peças.



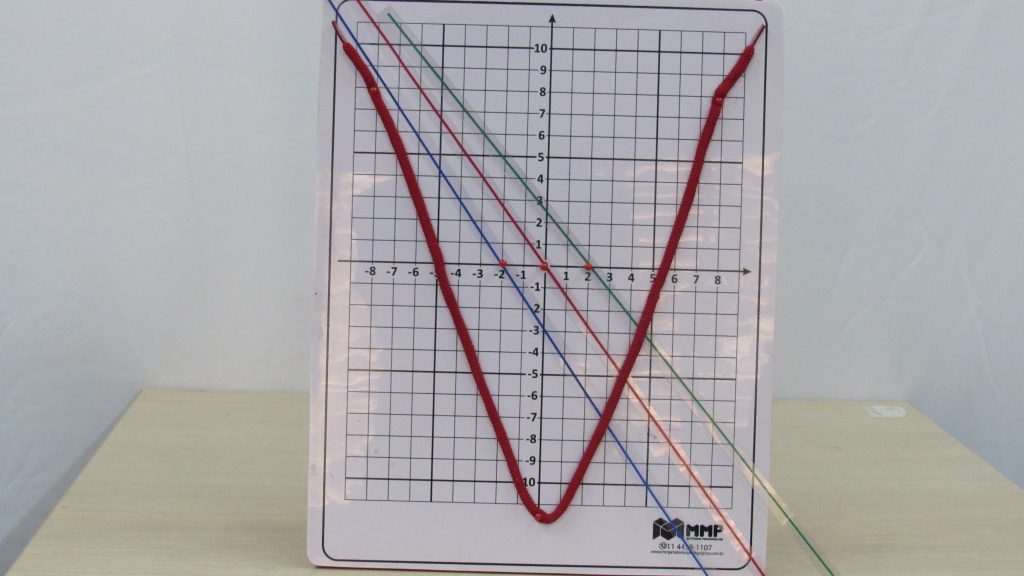
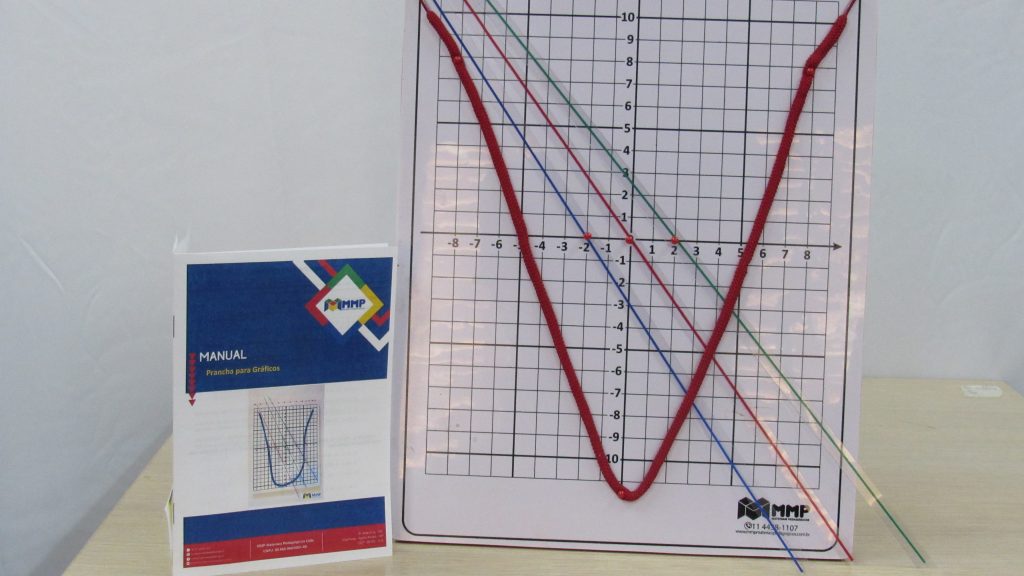
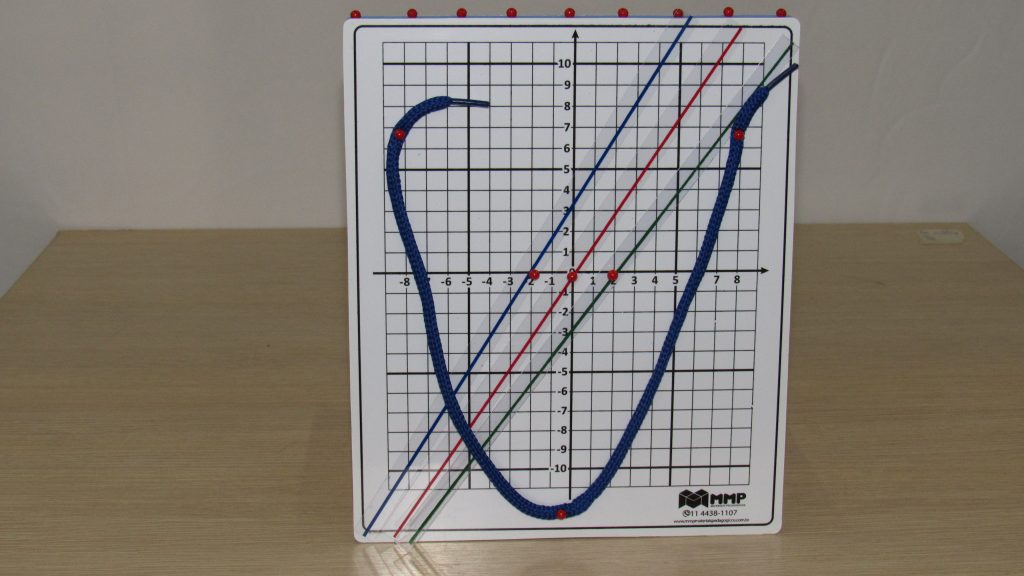
A prancha pra gráficos é um material didático ideal para localização de pontos de figuras geométricas planas. Solução de sistemas lineares. Permite a construção e análise de gráficos, notadamente para as funções de 1º e 2º graus. Desenho de retas, parábolas, varal de sinal, intersecção, funções, etc.
Esse incrível material aborda de forma bem ampla sobre o plano cartesiano, que é um assunto muito importante na matemática.



O Kit álgebra é um material pedagógico.
Ele possui quadrados e retângulos de várias cores em EVA que se combinam, tanto no tamanho como na mistura de cores, para serem feitas as operações algébricas (adição, subtração, produtos notáveis e casos de fatoração).
Excelente para a Iniciação ao estudo dos termos algébricos, suas operações, dedução de fórmulas algébricas; casos simples de produtos notáveis e de fatoração inclusive fatoração por agrupamento. Verificação da propriedade distributiva, etc.







É um jogo com tabuleiro e 5 dadinhos confeccionados em EVA 5 mm contendo nas faces expressões algébricas e peças em 2 cores: um lado azul e do outro vermelho, para: Operações com Polinômios, Produtos Notáveis e casos de Fatoração.
Objetivo/utilização: Aprender álgebra através do lúdico: adição e subtração de termos algébricos, produtos notáveis e casos de fatoração.
JOGO( Subtração)
Material necessário: 2 dadinhos quaisquer, peças do kit jogando com a Álgebra Procedimento: jogar dois dadinhos e pegar as peças correspondentes ao 1º e as simétricas ao segundo dadinho. Registre o fato matemático. Faça adições correspondentes e registre o resultado. Ganha quem ficar com o menor número de peças.











Um Sólido Geométrico é uma região do espaço limitada por uma superfície fechada. Dividem-se em dois grandes grupos: Poliedros e Não Poliedros.
Poliedros: São Sólidos limitados por superfícies planas. O cubo, as pirâmides e os prismas são exemplos de Poliedros.
Não Poliedros: São Sólidos que têm pelo menos uma face que não é plana. A esfera, o cone e o cilindro são exemplos de não poliedros.
São utilizados para exploração das suas formas e no reconhecimento de seus elementos através da visualização. Estes sólidos são indicados para dedução de fórmulas e calculo de áreas e volumes.
O que é:
Conjunto contendo 11 dos principais sólidos geométricos utilizados em sala de aula. Confeccionado em plástico em 4 cores diferentes.
SÓLIDOS
Pirâmide base Triangular (Tetraedro) altura 6cm aresta 8cm;
Pirâmide base Retangular altura 8cm lado 4 e lado 6cm;
Pirâmide base quadrada altura 8cm e lado 6cm;
Pirâmide base hexagonal altura 8cm e lado do hexágono 3cm;
Cone (altura 8cm e diâmetro 6cm);
Prisma de base triangular altura 8cm lado 6cm;
Prisma de base retangular altura 8cm lado 4 e lado 6cm;
Prisma de base hexagonal altura 8cm e lado do hexágono 3cm;
Cubo de aresta 6cm;
Esfera de diâmetro 6cm;
Cilindro altura 8cm e diâmetro 6cm.








O kit contém 30 cubinhos confeccionados em madeira para construção de poliedros e para Cálculos de Volumes. Tem também, um conjunto de 40 quadrados em EVA e 18 triângulos cuja área é a metade da área do quadrado, para realizar cálculo de área e perímetro de várias figuras geométricas planas.



















Quadrados retângulos confeccionados em EVA4 ou 5mm com uma face azul e a outra vermelha onde associamos os positivos que e negativos em tamanhos que se combinam sem serem múltiplos.
OBJETIVO/UTLILIZAÇÃO: Excelente recurso para visualização de propriedades com polinômios onde aparecem termos positivos e negativos.
Para as operações algébricas, produtos notáveis, casos de fatoração, divisão de polinômios, trabalhar com positivo e negativo, etc.